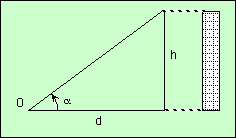
Calcul de la taille de l'image en fonction de l'angle et distance
On appelle tangente de l'angle α le rapport du côté opposé au côté adjacent.
On note tg la fonction tangente.
On voit tout de suite que si l'angle est nul, la hauteur de l'immeuble est nulle aussi. Si l'angle vaut 90°, la tangente (la hauteur) est infinie.
Pour quelle valeur de l'angle la hauteur vaut-elle 1 ? Si on refait un dessin montrant cette situation, on s'apperçoit qu'on a construit un carré, et que le triangle CPS est la moitié du carré. Donc l'angle recherché vaut la moitié d'un angle droit, 45°.
Supposons qu'on ait réussi à calculer les valeurs de cette fonction pour un grand nombre de valeurs de l'angle. Ces valeurs seront notées dans une table sous la forme :
| angle | tangente | angle | tangente |
| 0° | 0 | 50° | 1,19 |
| 5° | 0,0875 | 55° | 1,43 |
| 10° | 0,176 | 60° | 1,73 |
| 15° | 0,268 | 65° | 2,14 |
| 20° | 0,364 | 70° | 2,75 |
| 25° | 0,466 | 75° | 3,73 |
| 30° | 0,577 | 80° | 5,67 |
| 35° | 0,700 | 85° | 11,4 |
| 40° | 0,839 | 90° | infinie |
| 45° | 1,000 |
Alors, on peut calculer la hauteur d'un immeuble simplement en mesurant l'angle sous lequel on le voit et sa distance :
hauteur = distance tg α
